什麽是液體表麵張力？如何計算測量毛細管中的表麵張力？

由於(yu) 在流體(ti) 分子中發現的明顯張力效應或內(nei) 聚力而引起的特性稱為(wei) 表麵張力。因此，液體(ti) 顆粒顯示出與(yu) 不混溶表麵或液體(ti) 或氣體(ti) 界麵粘附的趨勢。或者，它可以理解為(wei) 在液體(ti) 界麵處自由存在的表麵能。

由於(yu) 表麵張力是線力，它通常表示為(wei) 穿過自由液體(ti) 表麵的每單位長度的力。

液體(ti) 表麵張力的較好例子可能是當一隻小螞蟻被一滴水纏住時，即使它隻是在一滴水中：由於(yu) 表麵的力量，螞蟻必須努力從(cong) 液體(ti) 中解脫出來水的張力。

測量表麵張力

參考下圖，可以看到典型的典型的流體(ti) 分子A由於(yu) 緊鄰A的相鄰分子施加的內(nei) 聚力而保持平衡狀態。

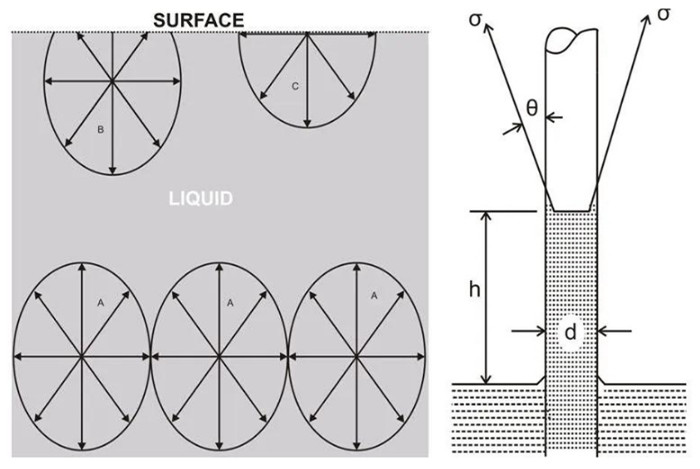
由於(yu) 相鄰分子相互施加的內(nei) 聚力相等且大小相反，因此它們(men) 抵消了這些作用，因此A上的淨力或合力變為(wei) 零。

然而，液體(ti) 表麵的分子向下表現出更大的內(nei) 聚力，因為(wei) 它們(men) 上方沒有分子。B上的合成內(nei) 聚力將更多地作用在向下的方向上。這種現象使液體(ti) 表麵與(yu) 拉伸的薄膜相當。

一般來說，與(yu) 液體(ti) 壓力和重力相比，表麵張力可以忽略不計；然而，封閉在狹窄區域或非常窄的柱子內(nei) 的流體(ti) 表現出強烈且顯著的內(nei) 聚趨勢，例如在毛細管、液滴、氣泡和通過多孔材料的液體(ti) 中。

當封閉在垂直或傾(qing) 斜的毛細管內(nei) 時，液體(ti) 的上升和下降稱為(wei) 毛細作用。

通過將流體(ti) 和毛細管壁之間形成的接觸角與(yu) 液柱上的平衡力聯係起來，可以理解這種現象。

參考下圖，很明顯，液麵與(yu) 毛細管壁之間的銳角接觸角構成了毛細作用的上升，反之亦然，而且液體(ti) 的內(nei) 聚力隨銳角減小而隨鈍角增大。

當封閉在直徑大於(yu) 1 cm 的管子和毛細管中時，上述對水和汞的作用變得無關(guan) 緊要。

測量毛細管中的表麵張力

如圖，我們(men) 看到毛細管上升，其中，向上的張力=管內(nei) 液柱的重量，

上式可以表述為(wei) ：

πd.σ.cosθ = πd2.h.ρg/4

因此，毛細上升可以計算為(wei) _, h = 4__σcosθ/__ρgd,_ 並且表麵張力可以通過求解：

σ = hρgd/4__cosθ

其中σ=由於(yu) 每單位長度的表麵張力而產(chan) 生的力，並且，

θ=管壁和液體(ti) 表麵之間的接觸角。

以水為(wei) 液體(ti) ，玻璃管，θ~0，

因此，玻璃管中有水，毛細上升變為(wei) ：

_h = 4__σ/_ρgd,

生成的表麵張力可以通過以下表達式進行評估：

σ = h__ρgd/4

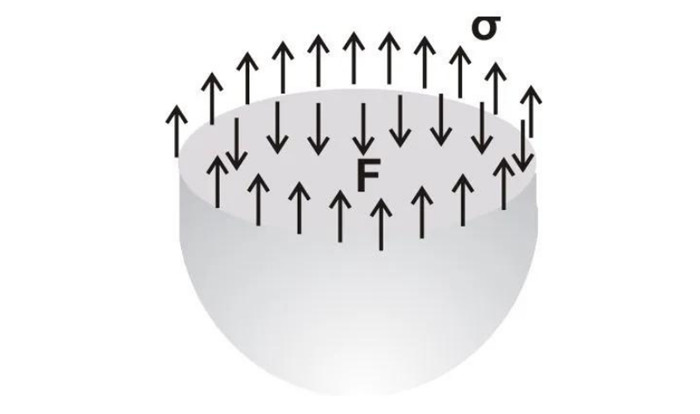
在液滴的情況下，液滴在封閉的液體(ti) 內(nei) 達到與(yu) 施加的表麵張力相等的壓力。

等於(yu) 我們(men) 得到的上述力，_πd.__σ = p._ πd2/4

最後，上述情況下測量表麵張力的公式變為(wei) ：

σ = pd/4

其中p = 壓力，d =液滴直徑。

上述解釋幫助我們(men) 理解與(yu) 液體(ti) 相關(guan) 的這一重要趨勢，並最終與(yu) 我們(men) 有關(guan) 什麽(me) 是表麵張力以及如何測量它。